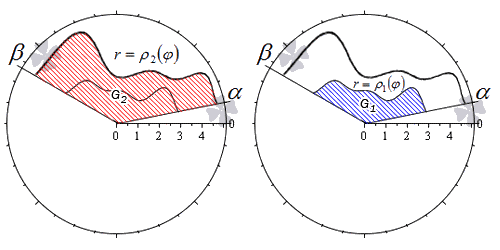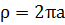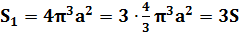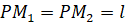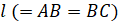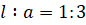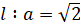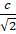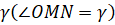площадь сектора спирали архимеда (4 видео)

Содержание

Вычисление площади фигуры в полярных координатах
Краткий обзор статьи
Полярная система координат и криволинейный сектор
Площадь криволинейного сектора — вывод формулы
Примеры вычисления площади криволинейного сектора
Площадь фигуры, которую ограничивает лемниската Бернулли
Площадь фигуры, границей которой является кардиоида
Площадь фигуры, которую ограничивает улитка Паскаля
Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль
Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов
Определение спирали Архимеда
Площадь сектора спирали архимеда
🔥 Видео

Видео:Площадь сектора и сегмента. 9 класс.Скачать

Вычисление площади фигуры в полярных координатах

В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y = f ( x ) , x = g ( y ) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.

Видео:Длина параболы и спирали Архимеда: что у них общего?Скачать

Краткий обзор статьи

Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.

Видео:Спираль Архимеда построениеСкачать

Полярная система координат и криволинейный сектор

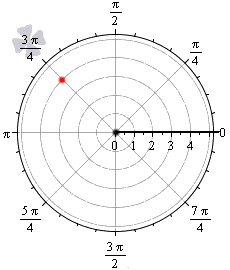
Точка, расположенная в полярной системе координат, имеет полярный угол φ 0 и полярный радиус r 0 ≥ 0 . Полярный угол φ 0 отсчитывается от полярной оси по часовой стрелке, а r 0 — это расстояние от заданной точки до начала координат.

На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ 0 = 3 π 4 и расстоянием до полюса r 0 = 4 .

Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.

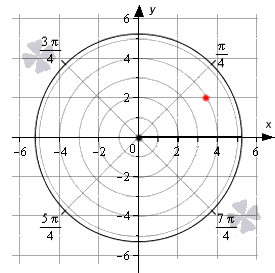
Задать связь полярных и декартовых координат можно соотношениями r = x 2 + y 2 φ = a r c t g y x , x ≠ 0 и обратно x = r · cos φ y = r · sin φ .

Координаты красной точки на чертеже 2 3 ; 2 . Положение этой точки задается углом φ 0 = a r c t g 2 2 3 = π 6 и расстоянием r 0 = 2 3 2 + 2 2 = 4 .

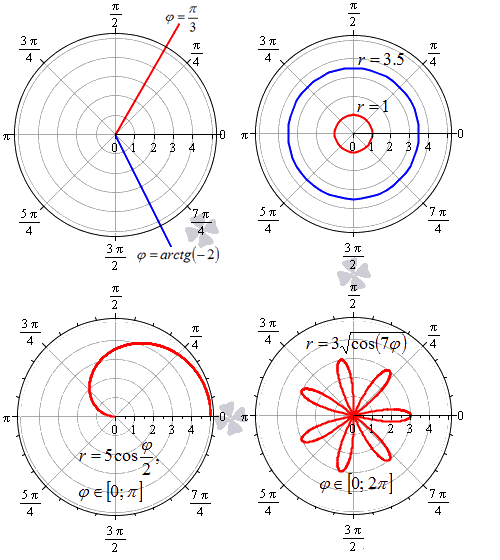
В полярной системе координат равенство φ = α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ = 0 . Равенство r = C > 0 задает окружность с центром в начале координат, где — это радиус.

Функция r = p ( φ ) , φ ∈ α ; β определяет некоторую линию в полярных координатах.

Следует учитывать тот факт, что с позиции геометрии функция r = p ( φ ) , φ ∈ α ; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ = φ 0 ∈ α ; β . Однако мы будем встречать и отрицательные значения r = p ( φ ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.

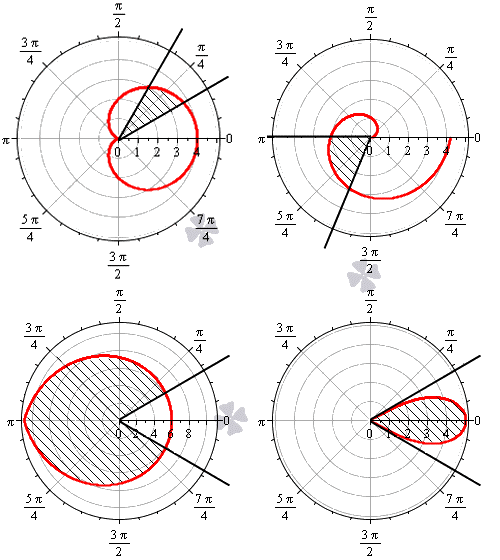
На рисунке мы изобразили несколько примеров линий в полярной системе координат.

Дадим определение криволинейному сектору.

Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ = α , φ = β и некоторой линией r = p ( φ ) ≥ 0 , непрерывной на участке α ; β .

На рисунке мы привели несколько примеров криволинейных секторов.

На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ = — π 6 , φ = π 6 , которые не являются ее границами.

Видео:§6 Спираль АрхимедаСкачать

Площадь криволинейного сектора — вывод формулы

Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: S к р у г о в о г о с е к т о р а = γ · R 2 2 . Задаем внутренний угол γ в радианах.

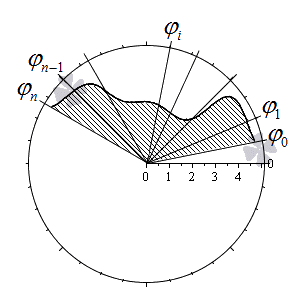
Разобьем криволинейный сектор на n частей такими лучами

φ = φ 1 , φ = φ 2 , . . . , φ = φ n — 1 , что α = φ 0 φ 1 φ 2 . . . φ n — 1 β и λ = m a x i = 1 , 2 , . . . , n φ i — φ i — 1 → 0 при n → + ∞ .

Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S ( G ) как сумму площадей секторов S ( G i ) на каждом из участков разбиения:

S ( G ) = ∑ i = 1 n S ( G i )

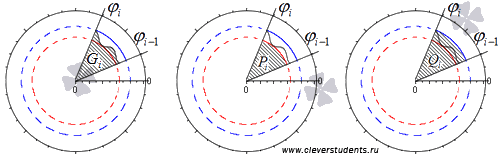
Обозначим наибольшее и наименьшее значения функции r = p ( φ ) на i -ом отрезке φ i — 1 ; φ i , i = 1 , 2 , . . . , n как R m i n i и R m a x i . На каждом из отрезков построим по два круговых сектора P i и Q i с максимальным и минимальным радиусами R m i n i и R m a x i соответственно.

Фигуры, которые являются объединением круговых секторов Q i , i = 1 , 2 , . . . , n ; P i , i = 1 , 2 , . . . , n , обозначим как P и Q соответственно.

Их площади будут равны S ( P ) = ∑ i = 1 n S ( P i ) = ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 и S ( Q ) = ∑ i = 1 n S ( Q i ) = ∑ i = 1 n 1 2 ( R m a x i ) 2 · φ i — φ i — 1 , причем S ( P ) ≤ S ( G ) ≤ S ( Q ) .

Так как функция r = p φ непрерывна на отрезке α ; β , то функция 1 2 p 2 φ будет непрерывна на этом отрезке. Если рассматривать S ( P ) и S ( Q ) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:

lim λ → 0 S ( P ) = lim λ → 0 S ( Q ) = S ( G ) ⇒ S ( G ) = lim λ → 0 ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 = = lim λ → 0 ∑ i = 1 n 1 2 ( R m a x i ) · φ i — φ i — 1 = 1 2 ∫ β α p 2 φ d φ

Формула для определения площади криволинейного сектора имеет вид:

S ( G ) = 1 2 ∫ β α p 2 φ d φ

Видео:Площадь круга - Доказательство Архимеда πR²Скачать

Примеры вычисления площади криволинейного сектора

Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.

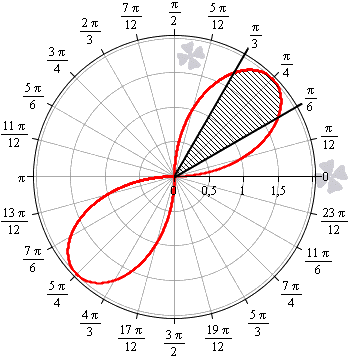
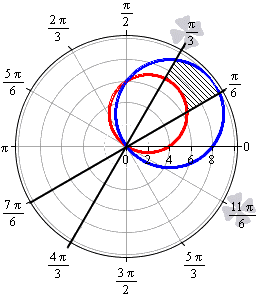
Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r = 2 sin 2 φ и лучами φ = π 6 , φ = π 3 .

Решение

Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r = 2 sin ( 2 φ ) положительна и непрерывна на отрезке φ ∈ π 6 , π 3 .

Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.

S ( G ) = 1 2 ∫ π 6 π 3 ( 2 sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 ( sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 · 1 — cos 4 φ 2 d φ = ∫ π 6 π 3 ( 1 — cos ( 4 φ ) ) d φ = φ — 1 4 sin ( 4 φ ) π 6 π 3 = = π 3 — 1 4 sin 4 π 3 — π 6 — 1 4 sin 4 π 6 = π 6 + 3 4

Ответ: S ( G ) = π 6 + 3 4

Задача упрощается в тех случаях, когда лучи φ = φ 1 , φ = φ 2 , ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.

Чаще встречаются задачи, где фигуру ограничивает лишь кривая r = p ( φ ) . В этих случаях применить формулу S ( G ) = 1 2 ∫ α β p 2 ( φ ) d φ сразу не получится. Для начала придется решить неравенство p ( φ ) ≥ 0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r = p φ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.

Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r = — 3 · cos 3 φ .

Решение

Функция определена для всех действительных значений аргумента. Решим неравенство — 3 · cos 3 φ ≥ 0 :

— 3 · cos 3 φ ≥ 0 ⇔ cos 3 φ ≤ 0 ⇔ cos φ ≤ 0 ⇔ ⇔ π 2 + 2 πk ≤ φ ≤ 3 π 2 + 2 πk , k ∈ Z

Построим функцию в полярных координатах на отрезке φ ∈ π 2 ; 3 π 2 (при k = 0 ). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.

Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π 2 + 2 πk и 3 π 2 + 2 πk соответственно для любого целого значения k .

S ( G ) = 1 2 ∫ π 2 3 π 2 ( — 3 · cos 3 φ ) d φ = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ

Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида K n ( x ) = sin x · cos n — 1 ( x ) n + n — 1 n K n — 2 ( x ) , где K n ( x ) = ∫ cos n ( x ) d x .

∫ cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 6 ∫ cos 4 φ d φ = = sin φ · cos 5 φ 6 + 5 6 sin φ · cos 3 φ 4 + 3 4 cos 2 φ d φ = = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 24 sin φ · cos φ 2 + 1 2 ∫ cos 0 φ d φ = = ∫ π 2 3 π 2 cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 sin φ · cos φ 48 + 15 φ 48 π 2 3 π 2 = = 15 48 · 3 π 2 — 15 48 · π 2 = 5 π 16

Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S ( G ) = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ = 9 2 · 5 π 16 = 45 π 32 .

Ответ: S ( G ) = 45 π 32

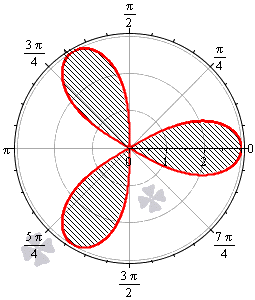
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.

Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r = 3 · cos ( 3 φ ) .

Решение

Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.

cos ( 3 φ ) ≥ 0 ⇔ — π 2 + 2 πk ≤ 3 φ ≤ π 2 + 2 πk , k ∈ Z — π 6 + 2 π 3 k ≤ φ ≤ π 6 + 2 π 3 k , k ∈ Z

Таким образом, период функции r = 3 · cos 3 φ равен 2 π 3 . Это значит, что фигура состоит из трех областей одинаковой площади.

Построим фигуру на графике.

Вычислим площадь одного участка, расположенного на интервале φ ∈ π 2 ; 5 π 6 (при k = 1 ):

1 2 ∫ π 2 5 π 6 9 cos ( 3 φ ) d φ = 1 2 · 3 sin ( 3 φ ) π 2 5 π 6 = 3 2 sin 3 · 5 π 6 — sin 3 · π 2 = 3 2 ( 1 — ( — 1 ) = 3

Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.

Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.

Видео:Площадь сектораСкачать

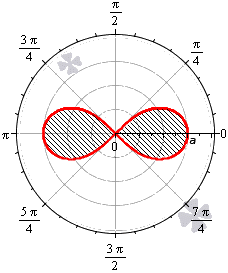
Площадь фигуры, которую ограничивает лемниската Бернулли

Лемниската Бернулли задается уравнением r = α · cos 2 φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при — π 4 + π · k ≤ φ ≤ π 4 + π · k , k ∈ Z .

Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.

Для вычисления площади используем нужную формулу:

S ( G ) = 2 · 1 2 ∫ — π 4 π 4 a 2 cos ( 2 φ ) 2 φ = a 2 2 ( sin ( 2 φ ) ) — π 4 π 4 = = a 2 2 sin 2 · π 4 — sin 2 · — π 4 = a 2

Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a .

Видео:Площадь 11 1Скачать

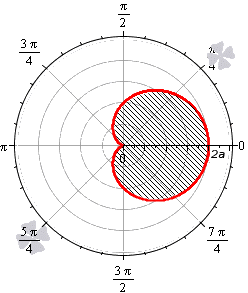
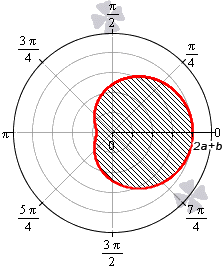
Площадь фигуры, границей которой является кардиоида

В полярной системе координат кардиоида задается уравнением вида r = 2 a ( 1 + cos φ ) . В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2 π . Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2 π больше нижнего.

Вычислим площадь фигуры, ограниченной кардиоидой r = 2 a ( 1 + cos φ ) , для φ ∈ 0 ; 2 π :

S ( G ) = 1 2 ∫ 0 2 π ( 2 a ( 1 + cos φ ) ) 2 d φ = 2 a 2 ∫ 0 2 π ( 1 + 2 cos φ + cos 2 φ ) d φ = = 2 a 2 ∫ 0 2 π 1 + 2 cos φ + 1 + cos 2 φ 2 d φ = = 2 a 2 ∫ 0 2 π 3 2 + 2 cos φ + cos ( 2 φ ) 2 d φ = = 2 a 2 3 2 φ + 2 sin φ + 1 4 sin 2 φ 0 2 π = 6 π · a 2

Видео:9 класс, 28 урок, Площадь кругового сектораСкачать

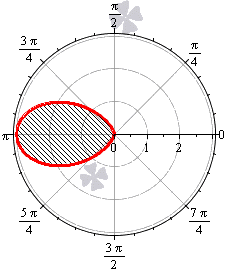
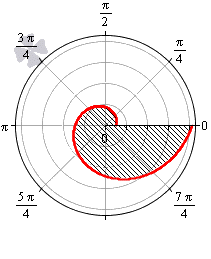
Площадь фигуры, которую ограничивает улитка Паскаля

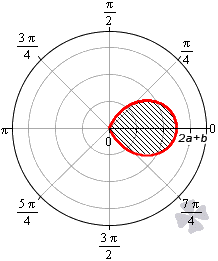
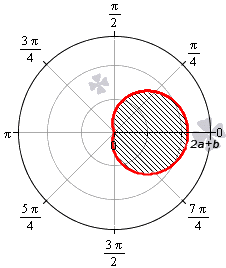
В полярной системе координат улитка Паскаля может быть задана уравнением r = b + 2 a · cos φ . В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b = 2 a .

Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.

При b — 2 a функция r = b + 2 a · cos φ будет отрицательной для любого значения угла φ .

При b = — 2 a улитка Паскаля имеет вид точки, которая совпадает с полюсом.

При — 2 a b 0 функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z .

При 0 b 2 a функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z . Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.

При b > 2 a функция r = b + 2 a · cos φ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже

Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b .

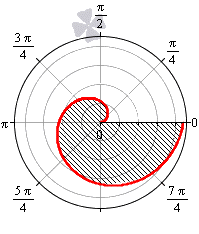
Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r = — 3 + 6 cos φ и r = 5 + 4 cos φ в полярной системе координат.

Решение

Формула r = — 3 + 6 cos φ соответствует фигуре, известной как улитка Паскаля..

Функция r = — 3 + 6 cos φ определена для всех значений угла φ . Нам необходимо выяснить, при каких φ функция будет неотрицательной:

— 3 + 6 cos φ ≥ 0 ⇔ cos φ ≥ 1 2 ⇔ — π 3 + 2 π k ≤ φ ≤ π 3 + 2 πk , k ∈ Z

Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:

S ( G ) = 1 2 ∫ — π 3 π 3 ( — 3 + 6 cos φ ) 2 d φ = 9 2 ∫ — π 3 π 3 ( 1 — 4 cos φ + 4 cos 2 φ ) d φ = = 9 2 ∫ — π 3 π 3 1 — 4 cos φ + 4 · 1 + cos 2 φ 2 d φ = = 9 2 ∫ — π 3 π 3 ( 3 — 4 cos φ + 2 cos ( 2 φ ) ) d φ = 9 2 · 3 φ — 4 sin φ + sin ( 2 φ — π 3 π 3 = = 9 2 · 3 · π 3 — 4 sin π 3 + sin 2 π 3 — 3 · — π 3 — 4 sin — π 3 + sin — 2 π 3 = = 9 2 · 2 π — 3 3

Улитка Паскаля, определяемая формулой r = 5 + 4 cos φ , соответствует пятому пункту. Функция r = 5 + 4 cos φ определена и положительна для всех действительных значений φ . Поэтому, площадь фигуры в этом случае равна:

S ( G ) = 1 2 ∫ 0 2 π ( 5 + 4 cos φ ) 2 d φ = 1 2 ∫ 0 2 π ( 25 + 40 cos φ + 16 cos 2 φ ) d φ = = 1 2 ∫ 0 2 π 25 + 40 cos φ + 16 · 1 + cos ( 2 φ ) 2 d φ = = 1 2 ∫ 0 2 π ( 33 + 40 cos φ + 8 cos ( 2 φ ) ) d φ = 1 2 · 33 φ + 40 sin φ + 4 sin ( 2 φ 0 2 π = = 1 2 · 33 · 2 π + 40 sin ( 2 π + 4 sin ( 4 π ) — 33 · 0 + 40 sin 0 + 4 sin 0 = 33 π

Ответ: S ( G ) = 33 π

Видео:Логарифмическая спиральСкачать

Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль

Сразу обратимся к примеру.

Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r = α φ , α > 0 , а вторая первым витком логарифмической спирали r = α φ , α > 1 .

Решение

Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.

Исходя из этого, найдем площадь фигуры по формуле:

S ( G ) = 1 2 ∫ 0 2 π ( α φ ) 2 d ϕ = α 2 2 ∫ 0 2 π φ 2 d φ = α 2 2 · φ 3 3 0 2 π = 4 α 3 π 3 3

Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:

S ( G ) = 1 2 ∫ 0 2 π ( α ϕ ) 2 d ϕ = 1 2 ∫ 0 2 π a 2 φ d φ = 1 4 ln a · a 2 φ 0 2 π = = 1 4 ln a · a 4 π — 1

Видео:Площади 12Скачать

Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов

Пусть фигура в полярной системе координат ограничена лучами φ = α , φ = β и непрерывными и неотрицательными на интервале φ ∈ α ; β функциями r = p 1 ( φ ) и r = p 2 ( φ ) , причем p 1 ( φ ) ≤ p 2 ( φ ) для любого угла φ = φ 0 ∈ α ; β .

Находим площадь фигуры по формуле S ( G ) = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ .

Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G 2 и G 1 .

Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:

S ( G ) = S ( G 2 ) — S ( G 1 ) = 1 2 ∫ α β p 2 2 ( φ ) d φ — 1 2 ∫ α β p 1 2 ( φ ) d φ = = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ

Последний переход возможен в силу третьего свойства определенного интеграла.

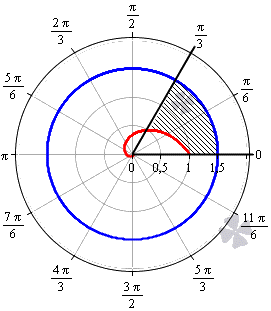
Необходимо вычислить площадь фигуры, которая ограничена линиями φ = 0 , φ = π 3 , r = 3 2 , r = 1 2 φ в полярной системе координат.

Решение

Построим заданную фигуру на графике.

Очевидно, что r = 3 2 больше r = 1 2 φ для любого φ ∈ 0 ; π 3 . Применяем полученную формулу для вычисления площади фигуры:

S ( G ) = 1 2 ∫ 0 π 3 3 2 2 — 1 2 φ 2 d φ = 1 2 ∫ 0 π 3 9 4 — 2 — 2 φ d φ = = 1 2 · 9 4 φ + 1 2 · 2 — 2 φ ln 2 0 π 3 = 1 2 · 9 4 φ + 1 ln 2 · 1 2 2 φ + 1 0 π 3 = = 1 2 · 9 4 · π 3 + 1 ln 2 · 1 2 2 · π 3 + 1 — 9 4 · 0 + 1 ln 2 · 1 2 2 · 0 + 1 = = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2

Ответ: S ( G ) = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2

А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.

Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y = 1 3 x , x = 3 x , окружностями ( x — 2 ) 2 + ( y — 3 ) 2 = 13 , ( x — 4 ) 2 + ( y — 3 ) 2 = 25 .

Решение

В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.

x = r · cos φ y = r · sin φ ⇒ y = 1 3 x ⇔ r · sin φ = r · cos φ 3 ⇔ t g φ = 1 3 ⇔ φ = π 6 + πk y = 3 x ⇔ r · sinφ = 3 · r · cosφ ⇔ tgφ = 3 ⇔ φ = π 3 + πk ( x — 2 ) 2 + ( y — 3 ) 2 = 13 ⇔ x 2 + y 2 = 4 x + 6 y ⇔ r = 4 cosφ + 6 sinφ ( x — 4 ) 2 + ( y — 3 ) 2 = 25 ⇔ x 2 + y 2 = 8 x + 6 y ⇔ r = 8 cosφ + 6 sinφ

Функция r = 8 cos φ + 6 sin φ больше r = 4 cos φ + 6 sin φ для любого φ ∈ π 6 ; π 3 . Вычисляем площадь фигуры в полярных координатах:

S ( G ) = 1 2 ∫ π 6 π 3 8 cos φ + 6 sin φ 2 — 4 cos φ + 6 sin φ 2 d φ = = 1 2 ∫ π 6 π 3 ( 48 cos 2 φ + 48 cos φ · sin φ ) d φ = = 24 ∫ π 6 π 3 cos 2 φ d φ + 24 ∫ π 6 π 3 cos φ · sin φ d φ = = 12 ∫ π 6 π 3 ( 1 + cos 2 φ ) d φ + 24 ∫ π 6 π 3 sin φ d ( sin φ ) = = 12 · φ + 1 2 sin ( 2 φ ) π 6 π 3 + 12 · sin 2 φ π 6 π 3 = = 12 · π 3 + 1 2 sin 2 π 3 — π 6 + 1 2 sin 2 π 6 + 12 · sin 2 π 3 — sin 2 π 6 = = 12 · π 6 + 12 · 3 2 2 — 1 2 2 = 2 π + 6

Видео:Площадь круга и АрхимедСкачать

Определение спирали Архимеда

Спираль Архимеда

Исторические сведения

Архимед (287 г. до н. э. — 212г. до н. э.) — древнегреческий математик, физик и инженер из Сиракуз (остров Сицилия). Он сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда важных изобретений.

Архимедова спираль была открыта Архимедом. Это произошло в III веке до н.э., когда он экспериментировал с компасом. Он тянул стрелку компаса с постоянной скоростью, вращая сам компас по часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же величину, на которую поворачивался компас, и между витками спирали сохранялось одно и то же расстояние.

Архимедову спираль использовали в древности, как наилучший способ определения площади круга. С ее помощью был улучшен древний греческий метод нахождения площади круга через измерение длины окружности. Спираль дала возможность более точного измерения длины окружности, а следовательно, и площади круга.

В III веке да нашей эры Архимед на основе своей спирали изобрёл винт, который успешно применяли для передачи воды в оросительные каналы из водоёмов, расположенных ниже. Позже на основе винта Архимеда создали шнек («улитку»). Его очень известная разновидность — винтовой ротор в мясорубке. Шнек используют в механизмах для перемешивания материалов различной консистенции.

Определение спирали Архимеда

Кривую можно рассматривать как траекторию точки, равномерно движущейся по лучу, исходящему из полюса, в то время как этот луч равномерно вращается вокруг полюса.

Представим себе циферблат часов с длинной стрелкой. Стрелка движется по окружности циферблата. А по стрелке в это время перемещается с постоянной скоростью маленький жучок. Траектория движения жучка представляет собой спираль Архимеда.

Построение спирали Архимеда

Чтобы понять, как получается спираль Архимеда, отметим на чертеже точку, которая является центром спирали Архимеда.

Построим из центра спирали окружность, радиус которой равен шагу спирали. Шаг спирали Архимеда равен расстоянию, которое проходит точка по поверхности круга за один его полный оборот.

Разделим окружность на несколько равных частей с помощью прямых линий. На первой линии откладываем одно деление, на второй-два деления, на третьей-три деления и т. д. Затем чертим соответствующее число дуг из центра окружности, проходящих через первое деление,2-ое и т. д.

Расстояния витков правой спирали, считая по лучу, равны ,а расстояния соседних витков, равны.

Уравнение Архимедовой спирали имеет вид:

где — радиус-вектор,- угол вращения,- шаг спирали.

Полярный угол мы отсчитываем от полярной оси, считая его положительным против часовой стрелки.

При вращении луча против часовой стрелки получается правая спираль (синяя линия) при вращении — по часовой стрелке — левая спираль (красная линия).

Полярный радиус-вектор мы будем брать как положительным, так и отрицательным; в первом случае его откладывают в направлении, определяемом углом , а во втором в противоположном направлении.

I.Вычислим площадь, описываемую полярным радиусом спирали при одном его обороте, если началу движения соответствует ,

Если мы найдем площадь круга радиуса ,то получим

То есть, мы получили, что площадь фигуры, ограниченной полярной осью и первым витком спирали, равна площади круга с радиусом, равным наибольшему из полярных радиусов витка.

II.Найдем длину первого витка спирали Архимеда.

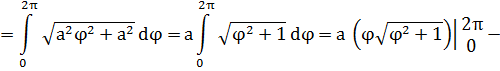
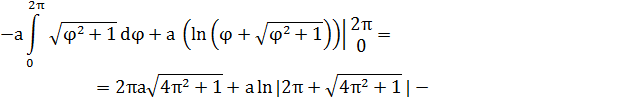
Логарифмическая спираль

Исторические сведения

Логарифмическая спираль была впервые описана Декартом (1638 г., опубликовано в 1657 г). Декарт искал кривую, обладающую свойством, подобным свойству окружности, так чтобы касательная в каждой точке образовывала с радиус-вектором в каждой точке один и тот же угол. Отсюда и название равноугольная. Он показал, что это условие равносильно тому, что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов. Отсюда и второе название: логарифмическая спираль. Независимо от Декарта она была открыта Э. Торричелли в 1644 г. Свойства логарифмической спирали исследовал Я. Бернулли (1692 г.). Её название предложено П. Вариньоном (1704 г.).

Гиперболическая спираль

Список литературы

1. Большой энциклопедический словарь «Математика»,

Гл. редактор Ю.В. Прохоров, Научное изд-во «Большая Российская Энциклопедия», М.: 1998

4. Маркушевич А.И., Замечательные кривые, М., 1978 г.

7. Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления; том I,II- М.: Наука, 1969

8. Математическая энциклопедия. Главный редактор И.М. Виноградов, т.3 — М.: «Советская энциклопедия», 1982

9. Графики функций. Справочник. Вирченко Н.А., Ляшко И.И., Швецов К.И.,1979 г.

Улитка Паскаля

Определение и построение

Даны: Точка O (полюс), окружность K диаметра OB=a (рис.6), проходящая через полюс (основная окружность; она показана на чертеже пунктиром), и отрезок . Из полюса O проводим произвольную прямую OP. От точки P, где прямая OP вторично пересекает окружность, откладываем в обе стороны от P отрезки . Геометрическое место точек M₁, M₂ (жирная линия на рис.6) называется улиткой Паскаля — в честь Этьена Паскаля (1588 — 1651), отца знаменитого французского ученого Блеза Паскаля (1623 — 1662).

Исторические сведения

Термин «улитка Паскаля» предложен Ж. Робервалем, современником и другом Паскаля. Роберваль рассматривал эту линию как один из видов обобщенной конхоиды.

Особенности формы

Улитка Паскаля симметрична относительно прямой OB. Эта прямая (ось улитки) пересекает улитку: 1) в точке O (если последняя принадлежит улитке); 2) в двух точках A, C (вершины). Форма линии зависит от соотношения между отрезками и .

1) Когда (линия 1 жирная; для неё ) улитка Паскаля пересекает сама себя в узловой точке O

Образуя две петли: внешнюю OHA₁GO и внутреннюю OH ‘ C₁G ‘ O. Угловой коэффициент касательных OD, OE в узловой точке:

Для построения касательных достаточно провести хорд OD, OE длины l в окружности K. Наиболее удаленным от оси точкам G, H внешней петли отвечает значение

Наиболее удаленным точкам G ‘ , H ‘ внутренней петли — значение

Соответствующее полярное значение полярного радиуса:

2) Когда (линия 2 на рис.6), внутренняя петля стягивается к полюсу и превращается в точку возврата, где движение по направлению луча OX сменяется движением в противоположном направлении. Наиболее удаленным от оси точкам L, M отвечают значения

Линия 2 называется кардиоидой, т.е. «сердцеобразной» (термин введен Кастиллоном в 1741г.). Она изображена отдельно на рис.7

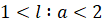
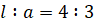
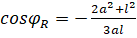
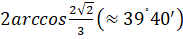
3) Когда (линия 3; для неё ), улитка Паскаля — замкнутая линия без самопересечения; оторвавшись от полюса, она заключает его внутри себя. Наиболее удаленным от оси точкам L ‘ , N ‘ отвечает значение . Лишившись точки возврата, улитка приобретает взамен точки перегиба R, Q, которым отвечает значение . Угол ROQ , под которым отрезок RQ виден из полюса, по мере возрастания сначала возрастает от нуля до ; этому значению соответствует . При дальнейшем увеличении угол ROQ убывает, стремясь к нулю при .

4) При точки перегиба, сливаясь с вершиной C пропадают (причем кривизна в точке C становится равной нулю). Улитка приобретает овальную форму и сохраняет ее при всех значениях

(линия 4; для нее ). Наиболее удаленным от оси точкам L » , N » отвечает значение

Свойства нормали

Нормаль улитки Паскаля в ее точке M (рис.7) проходит через точку N основной окружности K, диаметрально противоположную той точке P, где OM пересекается с основной окружностью.

Построение касательной

Чтобы провести касательную к улитке Паскаля в ее точке M, соежиняем последнюю с полюсом O. Точку N основной окрудности K, диаметрально противополжную точке P, соединяем с M. Прямая MN будет нормалью к улитке. Проводя MT MN, получим искомую касательную.

Задача

Дана улитка Паскаля с полюсом в точке O. Написать уравнения в прямоугольной и полярной системах координат.

Пусть начало координат — в полюсе O, ось OX направлена по лучу OB. Тогда уравнение в прямоугольной системе координат будет иметь вид:

Строго говоря, это уравнение представляет фигуру, состоящую из улитки Паскаля и полюса O, который может и не принадлежать определенному выше геометрическому месту (такой случай имеет место для линий 3 и 4 на рис.6).

Уравнение в полярной системе (O — полюс, OX — полярная ось):

где меняется от какого-либо значения до .

Лемниската Бернулли

Определение

Лемниската есть геометрическое место точке, для которых произведение расстояний от них до концов данно отрещка равно . Точки F₁, F₂ называются фокусами лемнискаты; прямая F₁F₂ — ее осью.

Исторические сведения

В 1694 г. Якоб Бернули в работе, посвященной теории приливов и отливов, использовал в качестве вспомогательного средства линию, которую он задает уравнением . Он отмечает сходство этой линии (рис.8) с цифрой 8 и узлообразной повязкой, которую он именует «лемниском». Отсюда называние лемниската. Лемниската получила широкую ивестность в 1718 г., когда итальянский математик Джулио Карло Фаньяно (1682 — 1766) установил, что интеграл, представляющий длину дуги лемнискаты, не выражается через элементарные функции, и тем не менее лемнискату можно разделить (с помощью линейки и циркуля) на n равных дуг при условии, что или или , где m — любое целое положительное число.

Лемниската есть частный вид линии Кассини. Однако, хотя линии Кассини получили всеобщую известность с 1749 г., тождественность «восьмерки Кассини» с лемнискатой Бернули была уставновлена лишь в 1806 г. (итальянским математиком Саладини).

Построение

Можно применять общий способ построя линия Кассини, но нижеизложенный способ (К. Маклорена) и проще и лучше. Строим (см. рис.) окружность радиуса с центром в точке F₁ (или F₂). Проводим произвольную секущую OPQ и откладываем на этой прямой в обе стороны от точки O отрезки OM и OM₁, равные хорде PQ. Точка M опишет одну из петель лемнискаты, точка M₁ — другую.

Особенности формы

Лемниската имеет две оси симметрии: прямую F₁F₂ (OX) и прямую OYOX. Точка O — узловая; обе ветви имеют здесь перегиб. Касательные в этой точке составляют с осью OX углы . Точки A₁,A₂ лемнискаты, наиболее удаленные от узла O (вершины лемнискаты), лежат на оси F₁F₂ на расстоянии от узла.

Свойства нормали.

Подяоный радиус OM лемнискаты образует с нормалью MN угол , вдвое больше полярного угла :

Другими словами: угол между осью OX и вектором NN ‘ внешней нормали лемнискаты в точке M равен утроенному полярному углу точки M:

Построение касательной

Чтобы построить касательную к лемнискате в ее точке M, проводим полярный радиус OM и строим . Перпендикуляр MT к прямой MN есть искомая касательная.

Задача

Написать уравнение лемнискаты Бернулли в прямоугольной системе координат (O — серидина отрезка F₁F₂) и в полярной системе координат (O — полюс).

Пусть точка O — начало координат ; ось OX направлена по F₁F₂. Тогда Уравнение в прямоугольной системе координат:

Если O — полюс, OX — полярная ось, то уравнение в полярной системе:

Угол изменяется в промежутках и .

1. Маркушевич А.И., Замечательные кривые, М., 1978 г., 48 стр. с ил.

2. Выгодский М.Я., Справочник по высшей математике, М.: АСТ: Астрель, 2008, 991 стр. с ил.

3. Атанасян Л.С. и Атанасян В.А., Сборник задач по геометрии. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. Ч. I, М., «Просвещение», 1973, 256 с.

4. Гурова А.Э. Замечательные кривые вокруг нас. М, 1989

5. Маркушевич А.И. Замечательные кривые. — М, 1978

Спираль Архимеда

Исторические сведения

Определение спирали Архимеда

Последнее изменение этой страницы: 2019-04-19; Просмотров: 567; Нарушение авторского права страницы

Видео:Лекальные кривые. Спираль Архимеда. Эвольвента окружности. ЦиклоидаСкачать

Площадь сектора спирали архимеда

Архимед родом из Сиракуз (Сицилия). Он был великим математиком и философом:
разработал методы нахождения площадей поверхностей и объемов различных тел и фигур,
открыл один из основных законов по статике и гидростатике, который в честь его носит имя «Закон Архимеда».
Архимед был замечательным изобретателем. Известны его изобретения:

архимедов винт;
определение состава сплавов взвешиванием различных фигур и тел.

Когда римляне напали на Сиракузы, Архимед организовал инженерную оборону города против римлян.

Стороны квадратов в «золотом прямоугольнике» равны соответственно числам Фибоначчи 1 1 2 3

Стороны квадратов в «золотом треугольнике» равны соответственно числам Фибоначчи 1 1 2 3 5 8 13

Леонардо Пизанский (Leonardo Pisano), Фибоначчи (Fibonacci) — итальянский математик (1180-1240). Родился в Пизе. Он долгое время жил на Востоке, где познакомился с математикой арабов. Достижения арабских математиков Фибоначчи продвигал в Западную Европу:

· В 1202 г. Леонардо написал труд под названием «Книга абака» (Liber Abaci). «Книга абака» стала первой математической энциклопедией средневековья, сыгравшей существенную роль в развитии математики в Европе.

· Самым главным трудом Леонардо считается Liber Abaci (1202).
В «Книге абака» Леонардо сформулировал задачу о кроликах:

«Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару? «

В результате решения этой задачи можно убедиться, что число пар в каждый из двенадцати последующих месяцев месяцев будет соответственно 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . П олучилась последовательность чисел, где каждое последующее число равно сумме двух предыдущих — известная последовательность Фибоначчи.

· В 1220 г. Фибоначчи издал сочинение: «Практика геометрии» (Practica geometria).

Фибоначчи решил множество сложных математических и практических проблем, опередив на столетия развитие науки. Е го идеи легли в основу огромного множества исследований, которыми занимается современная математическая наука.

Фибоначчи занимался проблемами торговли и решал практические задачи, например: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказал, что оптимальной является такая система гирь: 1, 2, 4, 8, 16.