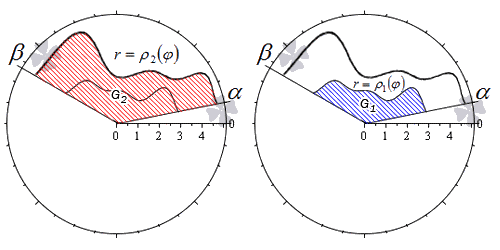площадь криволинейного сектора примеры

Видео:Площадь криволинейного сектора в параметрической формеСкачать

Площадь криволинейного сектора примеры

Площадь криволинейного сектора

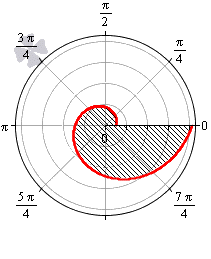
Пусть кривая L задана в полярной системе координат уравнением r = r(θ), α ≤ θ ≤ β (см. Рис. 3), причем функция r(θ) непрерывна и неотрицательна на сегменте [α, β]. Плоскую фигуру, ограниченную кривой L и двумя лучами, составляющими с полярной осью углы α и β, будем называть криволинейным сектором.

Докажем следующее утверждение. Криволинейный сектор представляет собой квадрируемую фигуру, площадь P которой может быть вычислена по формуле

(2)

Доказательство. Рассмотрим разбиение T сегмента [α, β] точками α = θ₀ ε > 0 эта разность может быть сделана меньше ε/2. Впишем теперь во внутреннюю веерообразную фигуру многоугольник Q_i с площадью S_i, для которого , и опишем вокруг внешней веерообразной фигуры многоугольник Q_d площадью S_d, для которого * . Очевидно, первый из этих многоугольников вписан в криволинейный сектор, а второй описан вокруг него. Так как справедливы неравенства

(3)

то, очевидно, S_d — S_i * Рассматриваемые веерообразные фигуры состоят из круговых секторов. Каждый сектор квадрируем, и поэтому квадрируемы и веерообразные фигуры. Поэтому для этих фигур можно найти многоугольники, площади S_i и S_d которых удовлетворяют указанным неравенствам.

Видео:ПОИ-8. Площадь криволинейного сектора в полярной системе координатСкачать

Вычисление площади фигуры в полярных координатах

В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y = f ( x ) , x = g ( y ) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.

Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Краткий обзор статьи

• Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
• Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
• В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Полярная система координат и криволинейный сектор

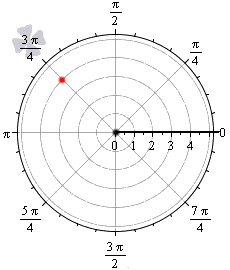
Точка, расположенная в полярной системе координат, имеет полярный угол φ 0 и полярный радиус r 0 ≥ 0 . Полярный угол φ 0 отсчитывается от полярной оси по часовой стрелке, а r 0 — это расстояние от заданной точки до начала координат.

На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ 0 = 3 π 4 и расстоянием до полюса r 0 = 4 .

Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.

Задать связь полярных и декартовых координат можно соотношениями r = x 2 + y 2 φ = a r c t g y x , x ≠ 0 и обратно x = r · cos φ y = r · sin φ .

Координаты красной точки на чертеже 2 3 ; 2 . Положение этой точки задается углом φ 0 = a r c t g 2 2 3 = π 6 и расстоянием r 0 = 2 3 2 + 2 2 = 4 .

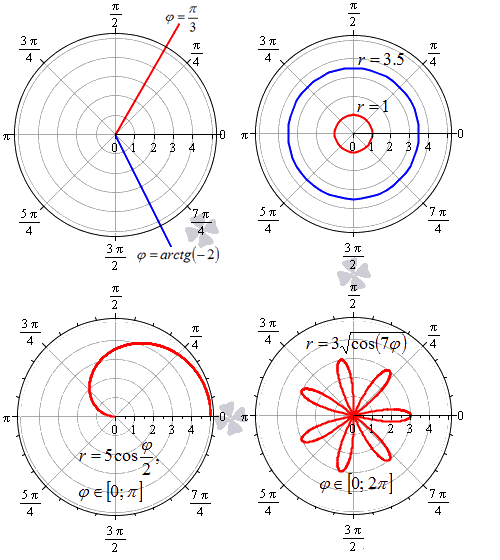
В полярной системе координат равенство φ = α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ = 0 . Равенство r = C > 0 задает окружность с центром в начале координат, где — это радиус.

Функция r = p ( φ ) , φ ∈ α ; β определяет некоторую линию в полярных координатах.

Следует учитывать тот факт, что с позиции геометрии функция r = p ( φ ) , φ ∈ α ; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ = φ 0 ∈ α ; β . Однако мы будем встречать и отрицательные значения r = p ( φ ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.

На рисунке мы изобразили несколько примеров линий в полярной системе координат.

Дадим определение криволинейному сектору.

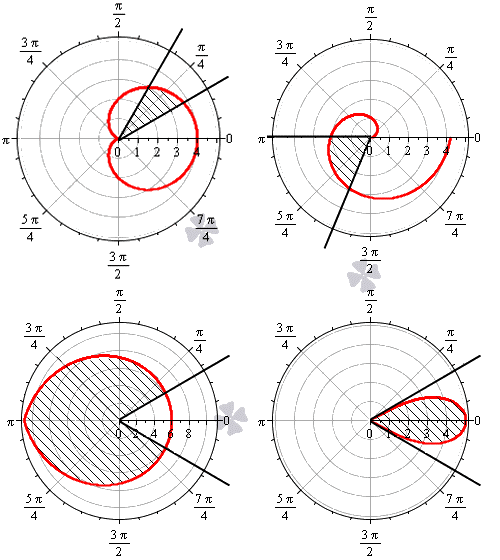
Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ = α , φ = β и некоторой линией r = p ( φ ) ≥ 0 , непрерывной на участке α ; β .

На рисунке мы привели несколько примеров криволинейных секторов.

На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ = — π 6 , φ = π 6 , которые не являются ее границами.

Видео:Площадь сектора и сегмента. 9 класс.Скачать

Площадь криволинейного сектора — вывод формулы

Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: S к р у г о в о г о с е к т о р а = γ · R 2 2 . Задаем внутренний угол γ в радианах.

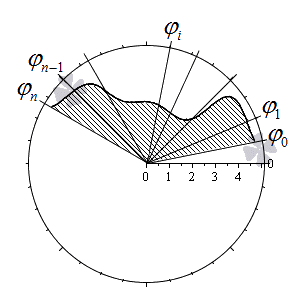
Разобьем криволинейный сектор на n частей такими лучами

φ = φ 1 , φ = φ 2 , . . . , φ = φ n — 1 , что α = φ 0 φ 1 φ 2 . . . φ n — 1 β и λ = m a x i = 1 , 2 , . . . , n φ i — φ i — 1 → 0 при n → + ∞ .

Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S ( G ) как сумму площадей секторов S ( G i ) на каждом из участков разбиения:

S ( G ) = ∑ i = 1 n S ( G i )

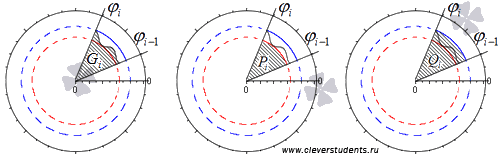
Обозначим наибольшее и наименьшее значения функции r = p ( φ ) на i -ом отрезке φ i — 1 ; φ i , i = 1 , 2 , . . . , n как R m i n i и R m a x i . На каждом из отрезков построим по два круговых сектора P i и Q i с максимальным и минимальным радиусами R m i n i и R m a x i соответственно.

Фигуры, которые являются объединением круговых секторов Q i , i = 1 , 2 , . . . , n ; P i , i = 1 , 2 , . . . , n , обозначим как P и Q соответственно.

Их площади будут равны S ( P ) = ∑ i = 1 n S ( P i ) = ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 и S ( Q ) = ∑ i = 1 n S ( Q i ) = ∑ i = 1 n 1 2 ( R m a x i ) 2 · φ i — φ i — 1 , причем S ( P ) ≤ S ( G ) ≤ S ( Q ) .

Так как функция r = p φ непрерывна на отрезке α ; β , то функция 1 2 p 2 φ будет непрерывна на этом отрезке. Если рассматривать S ( P ) и S ( Q ) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:

lim λ → 0 S ( P ) = lim λ → 0 S ( Q ) = S ( G ) ⇒ S ( G ) = lim λ → 0 ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 = = lim λ → 0 ∑ i = 1 n 1 2 ( R m a x i ) · φ i — φ i — 1 = 1 2 ∫ β α p 2 φ d φ

Формула для определения площади криволинейного сектора имеет вид:

S ( G ) = 1 2 ∫ β α p 2 φ d φ

Видео:Найти площадь фигуры, ограниченной линиями. Пример 1.Скачать

Примеры вычисления площади криволинейного сектора

Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.

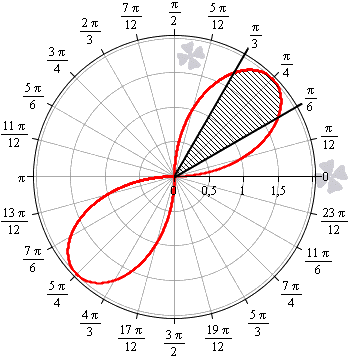
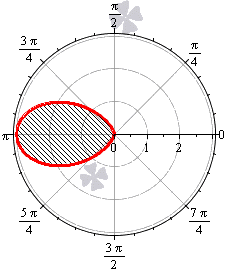
Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r = 2 sin 2 φ и лучами φ = π 6 , φ = π 3 .

Решение

Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r = 2 sin ( 2 φ ) положительна и непрерывна на отрезке φ ∈ π 6 , π 3 .

Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.

S ( G ) = 1 2 ∫ π 6 π 3 ( 2 sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 ( sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 · 1 — cos 4 φ 2 d φ = ∫ π 6 π 3 ( 1 — cos ( 4 φ ) ) d φ = φ — 1 4 sin ( 4 φ ) π 6 π 3 = = π 3 — 1 4 sin 4 π 3 — π 6 — 1 4 sin 4 π 6 = π 6 + 3 4

Ответ: S ( G ) = π 6 + 3 4

Задача упрощается в тех случаях, когда лучи φ = φ 1 , φ = φ 2 , ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.

Чаще встречаются задачи, где фигуру ограничивает лишь кривая r = p ( φ ) . В этих случаях применить формулу S ( G ) = 1 2 ∫ α β p 2 ( φ ) d φ сразу не получится. Для начала придется решить неравенство p ( φ ) ≥ 0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r = p φ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.

Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r = — 3 · cos 3 φ .

Решение

Функция определена для всех действительных значений аргумента. Решим неравенство — 3 · cos 3 φ ≥ 0 :

— 3 · cos 3 φ ≥ 0 ⇔ cos 3 φ ≤ 0 ⇔ cos φ ≤ 0 ⇔ ⇔ π 2 + 2 πk ≤ φ ≤ 3 π 2 + 2 πk , k ∈ Z

Построим функцию в полярных координатах на отрезке φ ∈ π 2 ; 3 π 2 (при k = 0 ). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.

Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π 2 + 2 πk и 3 π 2 + 2 πk соответственно для любого целого значения k .

S ( G ) = 1 2 ∫ π 2 3 π 2 ( — 3 · cos 3 φ ) d φ = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ

Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида K n ( x ) = sin x · cos n — 1 ( x ) n + n — 1 n K n — 2 ( x ) , где K n ( x ) = ∫ cos n ( x ) d x .

∫ cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 6 ∫ cos 4 φ d φ = = sin φ · cos 5 φ 6 + 5 6 sin φ · cos 3 φ 4 + 3 4 cos 2 φ d φ = = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 24 sin φ · cos φ 2 + 1 2 ∫ cos 0 φ d φ = = ∫ π 2 3 π 2 cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 sin φ · cos φ 48 + 15 φ 48 π 2 3 π 2 = = 15 48 · 3 π 2 — 15 48 · π 2 = 5 π 16

Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S ( G ) = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ = 9 2 · 5 π 16 = 45 π 32 .

Ответ: S ( G ) = 45 π 32

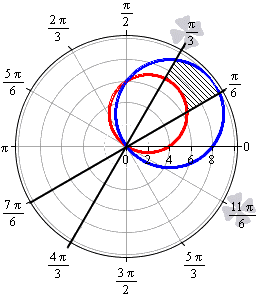
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.

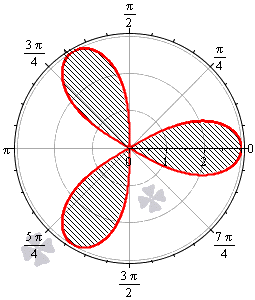
Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r = 3 · cos ( 3 φ ) .

Решение

Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.

cos ( 3 φ ) ≥ 0 ⇔ — π 2 + 2 πk ≤ 3 φ ≤ π 2 + 2 πk , k ∈ Z — π 6 + 2 π 3 k ≤ φ ≤ π 6 + 2 π 3 k , k ∈ Z

Таким образом, период функции r = 3 · cos 3 φ равен 2 π 3 . Это значит, что фигура состоит из трех областей одинаковой площади.

Построим фигуру на графике.

Вычислим площадь одного участка, расположенного на интервале φ ∈ π 2 ; 5 π 6 (при k = 1 ):

1 2 ∫ π 2 5 π 6 9 cos ( 3 φ ) d φ = 1 2 · 3 sin ( 3 φ ) π 2 5 π 6 = 3 2 sin 3 · 5 π 6 — sin 3 · π 2 = 3 2 ( 1 — ( — 1 ) = 3

Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.

Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.

Видео:Криволинейная трапеция и ее площадь. 11 класс.Скачать

Площадь фигуры, которую ограничивает лемниската Бернулли

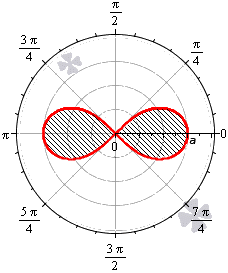
Лемниската Бернулли задается уравнением r = α · cos 2 φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при — π 4 + π · k ≤ φ ≤ π 4 + π · k , k ∈ Z .

Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.

Для вычисления площади используем нужную формулу:

S ( G ) = 2 · 1 2 ∫ — π 4 π 4 a 2 cos ( 2 φ ) 2 φ = a 2 2 ( sin ( 2 φ ) ) — π 4 π 4 = = a 2 2 sin 2 · π 4 — sin 2 · — π 4 = a 2

Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a .

Видео:Площадь криволинейного сектора в полярной системе координатСкачать

Площадь фигуры, границей которой является кардиоида

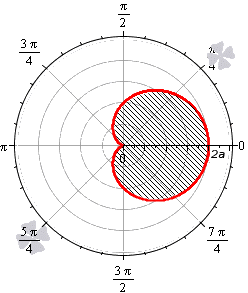
В полярной системе координат кардиоида задается уравнением вида r = 2 a ( 1 + cos φ ) . В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2 π . Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2 π больше нижнего.

Вычислим площадь фигуры, ограниченной кардиоидой r = 2 a ( 1 + cos φ ) , для φ ∈ 0 ; 2 π :

S ( G ) = 1 2 ∫ 0 2 π ( 2 a ( 1 + cos φ ) ) 2 d φ = 2 a 2 ∫ 0 2 π ( 1 + 2 cos φ + cos 2 φ ) d φ = = 2 a 2 ∫ 0 2 π 1 + 2 cos φ + 1 + cos 2 φ 2 d φ = = 2 a 2 ∫ 0 2 π 3 2 + 2 cos φ + cos ( 2 φ ) 2 d φ = = 2 a 2 3 2 φ + 2 sin φ + 1 4 sin 2 φ 0 2 π = 6 π · a 2

Видео:Найти площадь фигуры, ограниченной линиями. Пример 5.Скачать

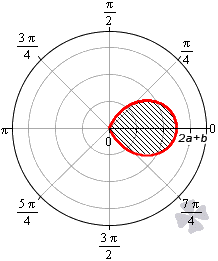
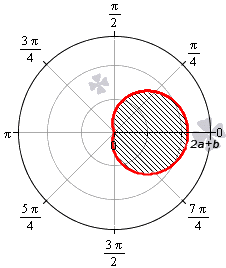
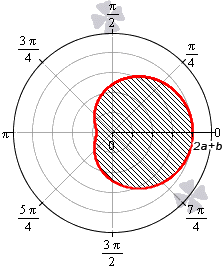
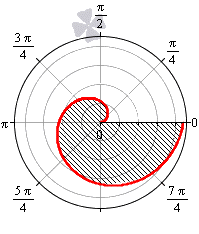
Площадь фигуры, которую ограничивает улитка Паскаля

В полярной системе координат улитка Паскаля может быть задана уравнением r = b + 2 a · cos φ . В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b = 2 a .

Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.

При b — 2 a функция r = b + 2 a · cos φ будет отрицательной для любого значения угла φ .

При b = — 2 a улитка Паскаля имеет вид точки, которая совпадает с полюсом.

При — 2 a b 0 функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z .

При 0 b 2 a функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z . Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.

При b > 2 a функция r = b + 2 a · cos φ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже

Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b .

Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r = — 3 + 6 cos φ и r = 5 + 4 cos φ в полярной системе координат.

Решение

Формула r = — 3 + 6 cos φ соответствует фигуре, известной как улитка Паскаля..

Функция r = — 3 + 6 cos φ определена для всех значений угла φ . Нам необходимо выяснить, при каких φ функция будет неотрицательной:

— 3 + 6 cos φ ≥ 0 ⇔ cos φ ≥ 1 2 ⇔ — π 3 + 2 π k ≤ φ ≤ π 3 + 2 πk , k ∈ Z

Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:

S ( G ) = 1 2 ∫ — π 3 π 3 ( — 3 + 6 cos φ ) 2 d φ = 9 2 ∫ — π 3 π 3 ( 1 — 4 cos φ + 4 cos 2 φ ) d φ = = 9 2 ∫ — π 3 π 3 1 — 4 cos φ + 4 · 1 + cos 2 φ 2 d φ = = 9 2 ∫ — π 3 π 3 ( 3 — 4 cos φ + 2 cos ( 2 φ ) ) d φ = 9 2 · 3 φ — 4 sin φ + sin ( 2 φ — π 3 π 3 = = 9 2 · 3 · π 3 — 4 sin π 3 + sin 2 π 3 — 3 · — π 3 — 4 sin — π 3 + sin — 2 π 3 = = 9 2 · 2 π — 3 3

Улитка Паскаля, определяемая формулой r = 5 + 4 cos φ , соответствует пятому пункту. Функция r = 5 + 4 cos φ определена и положительна для всех действительных значений φ . Поэтому, площадь фигуры в этом случае равна:

S ( G ) = 1 2 ∫ 0 2 π ( 5 + 4 cos φ ) 2 d φ = 1 2 ∫ 0 2 π ( 25 + 40 cos φ + 16 cos 2 φ ) d φ = = 1 2 ∫ 0 2 π 25 + 40 cos φ + 16 · 1 + cos ( 2 φ ) 2 d φ = = 1 2 ∫ 0 2 π ( 33 + 40 cos φ + 8 cos ( 2 φ ) ) d φ = 1 2 · 33 φ + 40 sin φ + 4 sin ( 2 φ 0 2 π = = 1 2 · 33 · 2 π + 40 sin ( 2 π + 4 sin ( 4 π ) — 33 · 0 + 40 sin 0 + 4 sin 0 = 33 π

Ответ: S ( G ) = 33 π

Видео:Интегралы №12 Вычисление площадейСкачать

Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль

Сразу обратимся к примеру.

Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r = α φ , α > 0 , а вторая первым витком логарифмической спирали r = α φ , α > 1 .

Решение

Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.

Исходя из этого, найдем площадь фигуры по формуле:

S ( G ) = 1 2 ∫ 0 2 π ( α φ ) 2 d ϕ = α 2 2 ∫ 0 2 π φ 2 d φ = α 2 2 · φ 3 3 0 2 π = 4 α 3 π 3 3

Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:

S ( G ) = 1 2 ∫ 0 2 π ( α ϕ ) 2 d ϕ = 1 2 ∫ 0 2 π a 2 φ d φ = 1 4 ln a · a 2 φ 0 2 π = = 1 4 ln a · a 4 π — 1

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов

Пусть фигура в полярной системе координат ограничена лучами φ = α , φ = β и непрерывными и неотрицательными на интервале φ ∈ α ; β функциями r = p 1 ( φ ) и r = p 2 ( φ ) , причем p 1 ( φ ) ≤ p 2 ( φ ) для любого угла φ = φ 0 ∈ α ; β .

Находим площадь фигуры по формуле S ( G ) = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ .

Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G 2 и G 1 .

Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:

S ( G ) = S ( G 2 ) — S ( G 1 ) = 1 2 ∫ α β p 2 2 ( φ ) d φ — 1 2 ∫ α β p 1 2 ( φ ) d φ = = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ

Последний переход возможен в силу третьего свойства определенного интеграла.

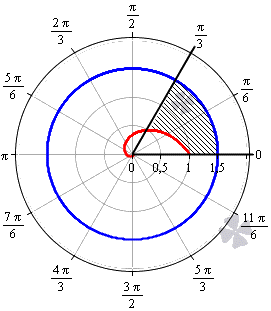
Необходимо вычислить площадь фигуры, которая ограничена линиями φ = 0 , φ = π 3 , r = 3 2 , r = 1 2 φ в полярной системе координат.

Решение

Построим заданную фигуру на графике.

Очевидно, что r = 3 2 больше r = 1 2 φ для любого φ ∈ 0 ; π 3 . Применяем полученную формулу для вычисления площади фигуры:

S ( G ) = 1 2 ∫ 0 π 3 3 2 2 — 1 2 φ 2 d φ = 1 2 ∫ 0 π 3 9 4 — 2 — 2 φ d φ = = 1 2 · 9 4 φ + 1 2 · 2 — 2 φ ln 2 0 π 3 = 1 2 · 9 4 φ + 1 ln 2 · 1 2 2 φ + 1 0 π 3 = = 1 2 · 9 4 · π 3 + 1 ln 2 · 1 2 2 · π 3 + 1 — 9 4 · 0 + 1 ln 2 · 1 2 2 · 0 + 1 = = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2

Ответ: S ( G ) = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2

А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.

Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y = 1 3 x , x = 3 x , окружностями ( x — 2 ) 2 + ( y — 3 ) 2 = 13 , ( x — 4 ) 2 + ( y — 3 ) 2 = 25 .

Решение

В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.

x = r · cos φ y = r · sin φ ⇒ y = 1 3 x ⇔ r · sin φ = r · cos φ 3 ⇔ t g φ = 1 3 ⇔ φ = π 6 + πk y = 3 x ⇔ r · sinφ = 3 · r · cosφ ⇔ tgφ = 3 ⇔ φ = π 3 + πk ( x — 2 ) 2 + ( y — 3 ) 2 = 13 ⇔ x 2 + y 2 = 4 x + 6 y ⇔ r = 4 cosφ + 6 sinφ ( x — 4 ) 2 + ( y — 3 ) 2 = 25 ⇔ x 2 + y 2 = 8 x + 6 y ⇔ r = 8 cosφ + 6 sinφ

Функция r = 8 cos φ + 6 sin φ больше r = 4 cos φ + 6 sin φ для любого φ ∈ π 6 ; π 3 . Вычисляем площадь фигуры в полярных координатах:

S ( G ) = 1 2 ∫ π 6 π 3 8 cos φ + 6 sin φ 2 — 4 cos φ + 6 sin φ 2 d φ = = 1 2 ∫ π 6 π 3 ( 48 cos 2 φ + 48 cos φ · sin φ ) d φ = = 24 ∫ π 6 π 3 cos 2 φ d φ + 24 ∫ π 6 π 3 cos φ · sin φ d φ = = 12 ∫ π 6 π 3 ( 1 + cos 2 φ ) d φ + 24 ∫ π 6 π 3 sin φ d ( sin φ ) = = 12 · φ + 1 2 sin ( 2 φ ) π 6 π 3 + 12 · sin 2 φ π 6 π 3 = = 12 · π 3 + 1 2 sin 2 π 3 — π 6 + 1 2 sin 2 π 6 + 12 · sin 2 π 3 — sin 2 π 6 = = 12 · π 6 + 12 · 3 2 2 — 1 2 2 = 2 π + 6

Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

Приложения определенного интеграла

Видео:Применение интегралов к вычислению площадей и длинСкачать

Вычисление площади плоской фигуры.

Плоская фигура и ее площадь.

Произвольное ограниченное множество точек плоскости будем называть плоской фигурой. Если плоскую фигуру можно представить как объединение конечного числа непересекающихся прямоугольников, то такую фигуру назовем клеточной. Подпрямоугольником будем понимать множество точек вида
$$
K = <(x, y): a_leq x leq b_, a_ leq y leq b_>nonumber
$$
или множество, получаемое из (K) удалением части границы (или всей границы) множества (K).

Площадью прямоугольника (K) назовем число ((b_-a_)(b_-a_)) независимо от того, принадлежат или не принадлежат множеству (K) его граничные точки, а площадью клеточной фигуры назовем сумму площадей прямоугольников, из которых составлена эта фигура.

Можно показать, что площадь клеточной фигуры не зависит от способа разбиения ее на прямоугольники. Нетрудно также убедиться в том, что площадь клеточной фигуры неотрицательна и обладает свойствами:

• аддитивности, то есть площадь объединения двух непересекающихся клеточных фигур равна сумме их площадей;
• инвариантности, то есть площади двух равных (конгруэнтных) клеточных фигур совпадают;
• монотонности, то есть если клеточные фигуры (G_) и (G_) таковы, что (G_ subset G_), то площадь фигуры (G_) не превосходит площади фигуры (G_).

Плоскую фигуру (G) назовем квадрируемой, если для любого (varepsilon > 0) найдутся клеточные фигуры (q) и (Q) такие, что
$$
q subset G subset Q,label
$$
$$
0 leq S(Q)-S(q) Теорема 1.

Для любой квадрируемой фигуры (G) число (S(G)) существует и единственно, причем
$$
S(G) = sup S(q) = inf S(Q).label
$$

(circ) Так как для любых клеточных фигур (q) и (Q), удовлетворяющих условию eqref, выполняется неравенство
$$
S(q) leq S(Q),nonumber
$$
то по теореме об отделимости существуют (sup S(q)) и (inf S(Q)) (супремум и инфимум берутся по всем клеточным фигурам, соответственно содержащимся в фигуре (G) и содержащим эту фигуру), причем
$$
S(q) leq sup S(q) leq inf S(Q) leq S(Q),label
$$
откуда
$$
S(q) leq sup S(q) leq S(Q),label
$$

Таким образом, число (S(G) = sup S(q)) удовлетворяет условию eqref.

Докажем единственность числа (S(G)). Предположим, что наряду с числом (S(G)) существует еще одно число (S'(G)), удовлетворяющее условию eqref, то есть
$$
S(q) leq S^(G) leq S(Q),label
$$
Тогда из eqref и eqref в силу свойств неравенств получаем, что
$$
|S(G)-S'(G)| leq S(Q)-S(q)label
$$
для любых клеточных фигур таких, что (q subset G subset Q). Так как (G) -квадрируемая фигура, то разность (S(Q)-S(q)) можно сделать сколь угодно малой в силу условия eqref, выбрав соответствующие фигуры (Q) и (q). Поэтому из eqref следует, что (S'(G) = S(G)). Таким образом, квадрируемая фигура (G) имеет площадь (S(G)), причем в силу eqref справедливо равенство eqref. (bullet)

Для того чтобы плоская фигура (G) была квадрируема, необходимо и достаточно, чтобы для любого (varepsilon > 0) существовали такие квадрируемые плоские фигуры (tilde) и (tilde), что
$$
tilde subset G subset tilde,quad 0 leq S(tilde)-S(tilde) Доказательство.

(circ) Необходимость условий eqref очевидна, так как по определению квадрируемой фигуры эти условия выполняются, если взять (tilde = q, tilde = Q), где (q) и (Q) — клеточные фигуры, удовлетворяющие соотношениям eqref, eqref.

Докажем достаточность. Фиксируя произвольное число (varepsilon > 0), найдем в силу eqref такие квадрируемые плоские фигуры (tilde) и (tilde), что
$$
tilde subset G subset tilde, 0 leq S(tilde)-S(tilde) Замечание 2.

Можно доказать, что площадь квадрируемой фигуры обладает свойствами аддитивности, инвариантности и монотонности (см. замечание 1).

Площадь криволинейной трапеции.

Одной из основных задач, приводящих к понятию определенного интеграла, является задача о площади криволинейной трапеции, то есть фигуры (G), задаваемой на плоскости (Oxy) условиями
$$
G = ,label
$$
где (f(x)) — функция, непрерывная на отрезке ([a, b]).

Криволинейная трапеция (G) — квадрируемая фигура, площадь которой (S = S(G)) выражается формулой
$$
S = intlimits_a^b f(x) dx,label
$$

(circ) Пусть (T = <x_, i = overline>) — разбиение отрезка ([a, b]), (M_) и (m_) — соответственно наибольшее и наименьшее значения функции (f) на отрезке (Delta_ = [x_, x_], Delta x_ = x_-x_, i = overline) (рисунок ниже).

Криволинейная трапеция

Рассмотрим клеточную фигуру (q), составленную из прямоугольников (q_ (i = overline)), таких, что длина основания (i)-го прямоугольника равна (Delta x_), а высота равна (m_).
Аналогично определяется клеточная фигура (Q), составленная из фигур (Q_), где (Q_) — прямоугольник, длина основания которого (Delta x_), а высота (M_, i = overline).
Очевидно, (q subset G subset Q), площади фигур (q) и (Q) соответственно равны
$$
S(q) = sum_^m_Delta x_,quad S(Q) = sum_^M_Delta x_.nonumber
$$
Заметим, что
$$
S(q) = s_, S(Q) = S_,label
$$
где (s_) и (S_) — соответственно нижняя и верхняя суммы Дарбу для функции (f) при разбиении (T) отрезка ([a, b]).

Так как функция (f(x)) непрерывна на отрезке ([a, b]), то в силу критерия интегрируемости для любого (varepsilon > 0) найдется такое разбиение (T) этого отрезка, что
$$
0 leq S_-s_ Замечание 3.

Ранее площадь (S) фигуры (G) была определена как предел интегральной суммы (sigma_ = displaystylesum_^f(xi_)Delta x_) при (l(T) rightarrow 0) при условии, что этот предел не зависит от разбиения (T) и выборки (xi = <xi_, i = overline>), где (xi_ in Delta_). Для непрерывной на отрезке ([a, b]) функции (displaystylelim_sigma_(xi) = intlimits_a^b f(x) dx), и поэтому оба определения площади приводят к одному и тому же результату.

Рассмотрим теперь фигуру (D) (рис. 37.1), ограниченную отрезками прямых (x = a) и (x = b) и графиками непрерывных на отрезке ([a, b]) функций (y = f_(x)) и (y = f_(x)), где (f_(x) leq f_(x)) при (x in [a, b]). Если (f_(x) geq 0) для всех (x in [a, b]), то площадь фигуры (D) равна разности площадей криволинейных трапеций (D_) и (D_), где (D_ = <(x, y): a leq x leq b, 0 leq y leq f_(x)>, i = 1,2). Поэтому площадь фигуры (D) выражается формулой
$$
S(D) = intlimits_a^b (f_(x)-f_(x)) dx.label
$$

Формула eqref остается в силе и в случае, когда не выполняется условие (f_(x) geq 0) для всех (x in [a, b]). Чтобы убедиться в этом, достаточно сдвинуть фигуру (D) вдоль положительного направления оси (Oy) на (y_ = displaystylevertmin_f_(x)vert) и воспользоваться тем, что площади равных фигур совпадают.

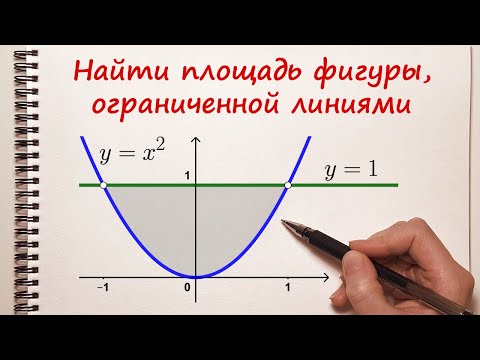
Найти площадь (S) фигуры, ограниченной эллипсом
$$
frac<x^><a^> + frac<y^><b^> = 1nonumber
$$

(triangle) Искомая площадь (S) равна (4sigma), где (sigma) (рис. 37.2) — площадь криволинейной трапеции, ограниченной осями (Ox), (Oy) и графиком функции (y = b displaystylesqrt<1-frac<x^><a^>>, 0 leq x leq a). По формуле eqref находим
$$
sigma = b intlimits_0^a sqrt<1-frac<x^><a^>> dx = ab intlimits_0^1 sqrt<1-t^> dt = frac pi abnonumber
$$
(см. пример здесь). Итак, площадь, ограниченная эллипсом с полуосями (a) и (b), равна
$$
S = pi abnonumber
$$
В частности, площадь круга радиуса (R) равна (pi R^). (blacktriangle)

Отсюда следует, что площадь кругового сектора (радиуса (R)), соответствующего центральному углу (alpha), равна
$$
frac<pi R^>alpha = frac<R^alpha>.nonumber
$$

Найти площадь фигуры, ограниченной параболой (y = 6x-x^) и прямой (y = x + 4).

(triangle) Парабола (y = 6x-x^) пересекается с прямой (y = x + 4) в точках (A) и В (рис. 37.3), абсциссы которых являются корнями уравнения (6x-x^ = x + 4). Решая это уравнение, находим его корни (x_ = 1, x_ = 4). Согласно формуле eqref искомая площадь (S) равна
$$
S = intlimits_1^4 ((6x-x^)-(x + 4)) dx = left(fracx^-left.frac<x^>-4xright)right|_^ = frac. blacktrianglenonumber
$$

Рис. 37.3

Площадь криволинейного сектора.

Пусть кривая (Gamma) задана в полярной системе координат уравнением
$$
rho = rho(varphi),quad alpha leq varphi leq beta,nonumber
$$
где (rho(varphi)) — неотрицательная и непрерывная на отрезке ([alpha, beta]) функция. Тогда плоскую фигуру (G), ограниченную кривой (Gamma) и, быть может, отрезками двух лучей, составляющих с полярной осью углы (alpha) и (beta) (рис. 37.4), назовем криволинейным сектором.

Рис. 37.4

Криволинейный сектор (G) — квадрируемая фигура, площадь которой (S) выражается формулой
$$
S = frac intlimits_^ rho^(varphi) dvarphi.label
$$

(circ) Пусть (T = <varphi_, i = overline>) — разбиение отрезка ([alpha, beta]), (m_) и (M_) — соответственно наименьшее и наибольшее значения функции (rho(varphi)) на отрезке (Delta_ = [varphi_, varphi_], i = overline). Обозначим через (q_) и (Q_) круговые секторы, ограниченные лучами (varphi = varphi_, varphi = varphi_) и дугами окружностей радиусов (m_) и (M_) соответственно (рис. 37.4). Если (q) — объединение фигур (q_, ldots, q_), а (Q) — объединение фигур (Q_, ldots, Q_), то (q subset G subset Q).Так как (q_) и (Q_) — квадрируемые фигуры, то (q) и (Q) также являются квадрируемыми фигурами, а их площади соответственно равны
$$
S(q) = frac sum_^m_^Delta varphi_quad mboxquad S(Q) = frac sum_^M_^Delta varphi_.nonumber
$$
Отсюда следует, что (S(q)) и (S(Q)) совпадают соответственно с нижней и верхней суммами Дарбу для функции (displaystylefrac rho^(varphi)) на отрезке ([alpha, beta]). Поэтому (следствие из теоремы о критерии интегрируемости)
$$
sup S(q) = inf S(Q) = frac intlimits_^ rho^(varphi) dvarphi.nonumber
$$
Это означает (теорема 2), что (G) — квадрируемая фигура, а ее площадь (S) выражается формулой eqref. (bullet)

Найти площадь фигуры (G), которая ограничена лемнискатой Бернулли (рис. 37.5), заданной уравнением
$$
rho^ = a^ cos 2varphi.nonumber
$$

(triangle) Фигура (G) симметрична относительно координатных осей. Площадь (sigma) той части фигуры (G), которая лежит в первом квадранте, согласно формуле eqref равна (sigma = displaystylefrac intlimits_0^ a^ cos 2varphi dvarphi). Поэтому искомая площадь (S = 4sigma = a^). (blacktriangle)

Видео:Найти площадь фигуры, ограниченной линиями. Пример 4.Скачать

Вычисление объема тела.

Тело и его объем.

Произвольное ограниченное множество точек пространства будем называть телом.

Основные определения и утверждения, относящиеся к телам, аналогичны соответствующим определениям и утверждениям, рассмотренным выше. Поэтому некоторые утверждения для тел будут опущены.

По аналогии с понятием клеточной фигуры назовем тело клеточным, если его можно представить как объединение конечного числа непересекающихся параллелепипедов, то есть тел вида
$$
M = <(x, y, z): a_leq x leq b_, a_ leq y leq b_, a_ leq z leq b_>,nonumber
$$
а также тел, получаемых из (M) удалением части границы (или всей границы) тела (M). Объемом параллелепипеда (M) назовем число ((b_-a_)(b_-a_)(b_-a_)), а объемом клеточного тела — сумму объемов составляющих его параллелепипедов.

Тело (Omega) будем называть кубируемым, если для любого (varepsilon > 0) найдутся клеточные тела (p) и (P) такие, что
$$
p subset Omega subset P,quad 0 leq V(P)-V(p) Рис. 37.6

Если основанием цилиндрического тела (Omega) служит плоская квадрируемая фигура (G), то тело (Omega) кубируемо, а его объем (V(Omega)) равен (S(G)h), где (S(G)) — площадь основания, (h) — высота тела (Omega). В частности, объем прямого кругового цилиндра равен (V = pi R^h), где (R) — радиус основания, (h) — высота цилиндра.

(circ) По определению плоской квадрируемой фигуры для любого (varepsilon > 0) существуют такие клеточные фигуры (q) и (Q), что
$$
q subset G subset Q,quad 0 leq S(Q)-S(q) Замечание 4.

Из свойства аддитивности объема и утверждения 3 следует, что ступенчатое тело, то есть тело, являющееся объединением конечного числа цилиндрических тел, кубируемо, если основания цилиндрических тел квадрируемы; при этом объем ступенчатого тела равен сумме объемов тел, из которых составлено ступенчатое тело.

Объем тела вращения.

Тело, образованное вращением вокруг оси (Ox) криволинейной трапеции (G) (условие eqref), где (f(x)) — функция, непрерывная на отрезке ([a, b]), кубируемо, а его объем (V) выражается формулой
$$
V = pi intlimits_a^b f^(x) dx.label
$$

(circ) Пусть (T, m_, M_, Delta x_, q, Q) — те же, что и в пункте про «площадь криволинейной трапеции». При вращении вокруг оси (Ox) фигур (q), (G), (Q) получаются тела вращения (p), (Omega), (P) такие, что
$$
p subset Omega subset P,nonumber
$$
причем объемы ступенчатых тел (p) и (P) соответственно равны
$$
V(p) = pi sum_^m_^Delta x_,quad V(P) = pi sum_^M_^Delta x_.nonumber
$$
Так как (V(p)) и (V(P)) равны соответственно нижней и верхней суммам Дарбу для функции (pi f^(x)) при разбиении (T) отрезка ([a, b]), то согласно следствию из теоремы о критерии интегрируемости
$$
sup V(p) = inf V(P) = pi intlimits_a^b f^(x) dx.nonumber
$$
Следовательно, (Q) — кубируемое тело (по теореме, аналогичной теореме 2), а его объем выражается формулой eqref. (bullet)

Найти объем тела, полученного при вращении вокруг оси (Ox) фигуры, ограниченной осью (Ox) и графиком функции (y = sin x, 0 leq x leq pi).

(triangle) По формуле eqref получаем (V = pi displaystyleintlimits_0^ sin^(x) dx = frac<pi^>). (blacktriangle)

Объем тела с заданными площадями поперечных сечений.

Пусть тело (Omega) заключено между плоскостями, перпендикулярными оси Ох и пересекающими эту ось в точках (x = a) и (x = b), где (a Рис. 37.7

Обозначим через (G_) фигуру, получаемую в сечении тела (Omega) плоскостью, перпендикулярной оси (Ox) и проходящей через точку (x in [a, b]) этой оси. Будем считать, что при любом (x in [a, b]) фигура (G_) квадрируема, а ее площадь (sigma (x)) — функция, непрерывная на отрезке ([a, b]). Кроме того, предположим, что при проектировании на плоскость, перпендикулярную оси (Ox), фигур (G_) и (G_), где (alpha, beta), — любые точки отрезка ([a, b]), получаются фигуры, одна из которых содержится в другой.

При указанных выше условиях тело (Omega) кубируемо, а его объем (V) выражается формулой
$$
V = intlimits_a^b sigma(x) dx.label
$$

(circ) Пусть (T = <x_, i = overline>) — разбиение отрезка ([a, b]), (m_) и (M_)-соответственно наименьшее и наибольшее значения функции (sigma(x)) на отрезке (Delta x_ = [x_, x_], Delta x_ = x_-x_, i = overline). Так как (sigma(x)) — непрерывная функция, то существуют точки (xi_ in Delta_) и (xi_’) такие, что (sigma(xi_) = m_, sigma(xi_’) = M_, i = overline).

Обозначим через (Omega_) ту часть тела (Omega), которая заключена между плоскостями (A_) и (A_), перпендикулярными оси (Ox) и проходящими соответственно через точки (x_) и (x_) (см. рис. 37.7).

Пусть (D_) и (D_’) — цилиндрические тела высотой (Delta x_), построенные на сечениях (G_<xi_>) и (G_<xi_’>) как на основаниях и расположенные между плоскостями (A_) и (A_). Тогда (D_ subset Omega_ subset D_’) а объемы тел (D_) и (D_’) соответственно равны
$$
V(D_) = m_Delta x_,quad V(D_’) = M_Delta x_.nonumber
$$
Если (p) — объединение тел (D_, ldots, D_), а (P) — объединение тел (D_’, ldots, D_’), то (p subset Omega subset P),
$$
V(p) = sum_^m_Delta x_,quad V(P) = sum_^M_Delta x_.nonumber
$$
Так как (sup V(p) = inf V(P) = displaystyleintlimits_a^b sigma(x) dx), то (Omega) — кубируемое тело, a его объем выражается формулой eqref. (bullet)

Вычислить объем эллипсоида (displaystylefrac<x^><a^> + frac<y^><b^> + frac<z^><c^> = 1).

(triangle) Воспользуемся тем, что площадь фигуры (G), получаемой в сечении эллипсоида плоскостью, параллельной плоскости (Oyz) и отстоящей от нее на расстоянии (x_), где (0 leq x_ leq a), равна
$$
S(x_) = pi bc (1-frac<x_^><a^>).label
$$
В самом деле, граница фигуры (G) — эллипс, задаваемый уравнениями
$$
frac<y^><b^> + frac<z^><c^> = 1-frac<x_^><a^>,quad x = x_
$$

Полуоси этого эллипса равны (blambda) и (clambda), где (lambda = displaystylesqrt<1-frac<x_^><a^>>). Используя пример 1, получаем формулу eqref, а по формуле eqref находим искомый объем эллипсоида:
$$
v = 2 intlimits_0^a S(x) dx = 2pi bc intlimits_0^a left(1-frac<x^><a^>right) dx = frac pi abc.nonumber
$$
Отсюда следует, что объем шара, радиус которого равен (R), выражается формулой (v = displaystylefrac pi R^) . (blacktriangle)

Видео:9 класс, 28 урок, Площадь кругового сектораСкачать

Вычисление длины дуги кривой.

Если кривая (Gamma), заданная уравнением
$$
Gamma = <boldsymbol= boldsymbol(t), alpha leq t leq beta>,label
$$
непрерывно дифференцируема, то ее длина (S) выражается формулой
$$
S = intlimits_^ |boldsymbol'(t)| dt.label
$$

(circ) Ранее было доказано, что непрерывно дифференцируемая кривая (Gamma) спрямляема (имеет длину), а производная переменной длины дуги (s(t)) этой кривой выражается формулой
$$
s'(t) dt = |boldsymbol'(t)|.label
$$
Пусть (S) — длина всей кривой (Gamma); тогда, используя равенство eqref и формулу Ньютона-Лейбница, получаем
$$
intlimits_^ |boldsymbol'(t)| dt = intlimits_^ s'(t) dt = s(beta)-s(alpha) = S.nonumber
$$
так как (s(beta) = S), a (s(alpha) = 0). (bullet)

Если (boldsymbol(t) = (x(t), y(t), z(t))), то формула eqref принимает вид
$$
S = intlimits_^ sqrt<(x'(t))^+(y'(t))^+(z'(t))^> dt.label
$$
а если (Gamma)-плоская кривая, заданная уравнением
$$
y = f(x),quad a leq x leq b,nonumber
$$
то ее длина выражается формулой
$$
S = intlimits_a^b sqrt<1 + (f^(x))^> dx.label
$$

Найти длину кривой (y = operatorname x, 0 leq x leq a).

(triangle) Применяя формулу eqref, находим
$$
S = intlimits_0^a sqrt<1 + operatorname^x> dx = intlimits_0^a operatorname x dx = operatorname a. blacktrianglenonumber
$$

Видео:💯Площадь сектора - куска пиццыСкачать

Вычисление площади поверхности вращения.

Пусть (f(x)) — неотрицательная и непрерывная на отрезке ([a, b]) функция, (T = <x_, i = overline>) — разбиение отрезка ([a, b]), (L_) — ломаная с вершинами (A_(x_, f(x_)), i = overline), соединяющая последовательно точки (A_, A_, ldots A_) (рис. 37.8), (l_) — длина отрезка (mathcal_ = [A_, A_]) — (i)-го звена ломаной (L_). Тогда
$$
l_ = sqrt<(x_-x_)^ + (f(x_)-f(x_))^>.label
$$

При вращении вокруг оси (Ox) звена (mathcal_) образуется боковая поверхность усеченного конуса (цилиндра в случае, когда (f(x_) = f(x_))). Площадь этой поверхности, как известно из курса элементарной геометрии, равна
$$
p_ = pi (y_ + y_)l_,quad y_ = f(x_),quad k = overline,nonumber
$$
откуда следует, что площадь (mathcal

_) поверхности, получаемой при вращении ломаной (L_) вокруг оси (Ox), равна
$$
mathcal

_ = sum_^(y_ + y_)l_.label
$$

Если существует
$$
lim_ mathcal

_ = mathcal

.label
$$
где (l(T)) — мелкость разбиения (T), а (mathcal

_) определяется формулой eqref, то число (mathcal

) называют площадью поверхности вращения, то есть площадью поверхности, образующейся при вращении вокруг оси (Ox) графика функции (y = f(x), a leq x leq b).

Рис. 37.8

Если функция (f) имеет непрерывную производную на отрезке ([a, b]), то предел eqref существует, а площадь (mathcal

) поверхности вращения выражается формулой
$$
mathcal

= 2pi intlimits_a^b f(x) sqrt<1 + (f'(x))^> dx.label
$$

(circ) Из формул eqref и eqref следует, что
$$
mathcal

_ = pisum_^sqrt<(x_-x_)^ + (y_-y_)^>(y_ + y_),label
$$
где (y_i=f(x_i)). По теореме Лагранжа
$$
y_-y_ = f'(xi_)Delta x_,label
$$
где (xi_ in Delta_ = [x_, x_]), (Delta x_ = x_-x_). Поэтому формулу eqref можно записать в виде
$$
mathcal

_ = pi sum_^(y_ + y_) sqrt<1 + (f'(xi_))^>Delta x_.label
$$
Прибавим и вычтем в правой части равенства eqref интегральную сумму для интеграла eqref, соответствующую разбиению (T) и выборке (xi = xi_ (i = overline)), указанной формулой eqref, то есть сумму
$$
sigma_ (xi, g)= 2pi sum_^(f(xi_))sqrt<1 + (f'(xi_))^>Delta x_.label
$$
где (g(x) = 2pi f(x)displaystylesqrt<1 + (f'(x))^>). Заметим, что в силу непрерывности функции (g) для любой выборки (xi) существует
$$
lim_ sigma_ (xi, g) = 2pi intlimits_a^b f(x) sqrt<1 + (f'(x))^> dx.nonumber
$$
Поэтому для доказательства формулы eqref достаточно показать, что
$$
omega = mathcal

_-sigma_ (xi, g) rightarrow 0 mbox l(T) rightarrow 0.label
$$
Из eqref и eqref следует, что
$$
omega = pi sum_^(y_ + y_-2f(xi_i)) sqrt<1 + (f'(xi_))^>Delta x_.label
$$
При оценке величины (omega) воспользуемся тем, что функция (a) равномерно непрерывна на отрезке ([a, b]), то есть для любого (varepsilon > 0) существует (delta_ > 0) такое, что для любых точек (x’), (x″) из отрезка ([a, b]), удовлетворяющих условию (|x’-x″| 0) будет выбрано ниже.

Пусть разбиение (T) удовлетворяет условию (l(T) = displaystylemax_ Delta x_ 0) такое, что (0 0) существует (delta_ > 0) такое, что для каждого разбиения (T), мелкость (l(T)) которого удовлетворяет условию (l(T) Пример 7.

Пользуясь формулой eqref, вычислить площадь (mathcal

) поверхности сферического пояса высоты (h), если радиус сферы равен (R).

(triangle) Сферический пояс высоты (h) можно получить вращением дуги полуокружности, заданной уравнением (y = f(x) = displaystylesqrt<R^-x^>, a leq x leq b), где ([a, b] subset [-R, R], b-a = h), вокруг оси (Ox) (рис. 37.9). Так как (f'(x) =-displaystylefrac<sqrt<R^-x^>>), то (1 + (f'(x))^ = displaystylefrac<R^><R^-x^>), (f(x)sqrt<1 + (f'(x))^> = R) и по формуле eqref получаем (mathcal

_ = 2pi displaystyleintlimits_a^b R dx = 2pi R(b-a) = 2pi Rh). В частности, площадь поверхности сферы радиуса (R) равна (4pi R^). (blacktriangle)

Рис. 37.9

Видео:Найти площадь фигуры, ограниченной линиями. Пример 2.Скачать

Применение определенного интеграла при решении физических задач.

Определенный интеграл широко применяется при решении различных физических задач. С помощью определенного интеграла можно вычислять: путь, пройденный материальной точкой, если известна скорость движения; работу переменной силы; силу давления жидкости на плоскую фигуру; статические моменты и координаты центра масс плоской кривой и плоской фигуры и так далее.

Пусть плоская пластинка (G), имеющая форму криволинейной трапеции, определяемой условиями eqref, погружена вертикально в жидкость с плотностью (rho) так, что ее боковые стороны параллельны поверхности жидкости и удалены от уровня жидкости на расстояния (a) и (b) (рис. 37.10). Требуется найти силу давления жидкости на пластинку.

Рис. 37.10

Из курса физики известно, что если пластинка погружена в жидкость и расположена горизонтально на расстоянии (h) от поверхности жидкости, то сила давления (mathcal

) на одну из сторон пластинки равна
$$
mathcal

= g rho hS,nonumber
$$
где (S) — площадь пластинки, (g) — ускорение силы тяжести. Таким образом, сила давления — линейная функция от глубины погружения пластинки. Поэтому естественно разбить пластинку (G) на части прямыми, параллельными поверхности жидкости (оси (Oy)).

Пусть (T = <x_, i = overline>) — разбиение отрезка ([a, b]). Прямыми, проведенными через точки (x_ (i = overline)), разобьем фигуру (G) на (n) частей (полосок) (G_ (i = overline)). Выделим полоску (G_), ограниченную прямыми (x = x_) и (x = x_) (рис. 37.10). Площадь этой полоски приближенно равна площади прямоугольника с основанием (Delta x_) и высотой (f(x_)), глубину погружения всех точек полоски (G_) можно считать равной (x_). Поэтому сила давления жидкости на полоску (G_) приближенно равна
$$
g rho x_f(x_)Delta x_,nonumber
$$
а сумма
$$
mathcal

_ = sum_<substack>^<substack> g rho x_f(x_)Delta x_nonumber
$$
приближенно равна силе давления жидкости на пластинку (G).

Если (l(T) rightarrow 0), где (l(T)) — мелкость разбиения (T), а функция (f) непрерывна на отрезке ([a, b]), то (mathcal

_ rightarrow mathcal

), где
$$
mathcal

= g intlimits_a^b rho x f(x) dx.label
$$
Число (mathcal

) выражаемое формулой eqref, называют силой давления жидкости на пластинку (G).

Вычислить силу давления (mathcal

) жидкости с плотностью (rho) на вертикальную стенку, имеющую форму полукруга радиуса (R) и погруженную в жидкость так, что диаметр полукруга расположен на поверхности жидкости (рис. 37.11).

Рис. 37.11

(triangle) Выберем систему координат так, как указано на рис. 37.11. Пользуясь формулой eqref, где (f(x) = sqrt<R^-x^>, a = 0, b = R), получаем
$$
mathcal

= 2g rho intlimits_0^R x sqrt<R^-x^> dx =-left.frac g rho (R^-x^)^right|_^ = frac R^. blacktrianglenonumber
$$

🎥 Видео

Построение кривой в полярной системе координатСкачать

Найти площадь фигуры, ограниченной линиями. Пример 3.Скачать